デルタ関数型ポテンシャルの問題はよく出題される。
例えば令和2年度北大院試や、平成24年度東工大院試
今回はこのようなデルタ関数型ポテンシャルの境界条件について考える。
デルタ関数型ポテンシャル
ポテンシャルの形は、デルタ関数を用いて
$$V(x) = A\delta (x) \hspace{4mm}(A : {\rm const})$$
と書ける。デルタ関数は
$$\begin{align} \delta(x) = \left\{\begin{matrix}\infty &(x=0)\\ 0 & (x\neq 0)\end{matrix}\right.\end{align}$$
となる値を持つ関数である。
シュレディンガー方程式
$$\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + A\delta (x) \right)\psi(x) = E\psi(x) $$
この式の両辺を\([-\varepsilon,\varepsilon]\)(\(\varepsilon >0\))の範囲で積分すると
$$-\frac{\hbar^2}{2m}\int^{\varepsilon}_{-\varepsilon}\frac{d^2}{dx^2}\psi(x) dx + A\int^{\varepsilon}_{-\varepsilon}\delta (x)\psi(x)dx = E\int^{\varepsilon}_{-\varepsilon}\psi(x) dx$$
$$-\frac{\hbar^2}{2m}\left(\left.\frac{d\psi(x)}{dx}\right|_{x=\varepsilon} – \left.\frac{d\psi(x)}{dx}\right|_{x=-\varepsilon}\right) + A\psi (0) = E\int^{\varepsilon}_{-\varepsilon}\psi(x) dx$$
となる。ここで、\(\varepsilon\to 0\)とすると、右辺は波動関数が連続であることから0となる。従って
$$-\frac{\hbar^2}{2m}\left(\left.\frac{d\psi(x)}{dx}\right|_{x=+0} – \left.\frac{d\psi(x)}{dx}\right|_{x=-0}\right) + A\psi (0) = 0\tag{\(\star\)}$$


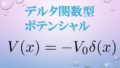
コメント