【院試解答】平成24年度　東工大理学院物理学系　午後第3問

問題はこちら

式など

$$V(x) = -Z \delta (x – x_0) \tag{i}$$

$$\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x) \right)\psi(x) = E\psi(x) \tag{ii}$$

解答

$$\frac{\psi'(x_0 – 0)}{\psi(x_0)} – \frac{\psi'(x_0 + 0)}{\psi(x_0)} = 2k_0 \tag{iii}$$

　\(x_0\)の近傍\(x_0 \pm \varepsilon\)の範囲でシュレディンガー方程式(ii)を積分すると

$$ \int^{x_0 + \varepsilon}_{x_0 – \varepsilon}\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x) \right)\psi(x)dx = \int^{x_0 + \varepsilon}_{x_0 – \varepsilon} E\psi(x) dx$$

$$-\frac{\hbar^2}{2m} (\psi'(x_0 + \varepsilon) – \psi'(x_0 – \varepsilon)) -Z \int^{x_0 + \varepsilon}_{x_0 – \varepsilon} \delta (x – x_0)\psi(x) dx = \int^{x_0 + \varepsilon}_{x_0 – \varepsilon} E\psi(x) dx \tag{4}$$

となる。ここで、

$$\int^{x_0 + \varepsilon}_{x_0 – \varepsilon} \delta (x – x_0) \psi(x)dx = \psi(x_0)$$

であり、\( \varepsilon \rightarrow 0\)とすると式(4)の右辺は0となる。よって

$$-\frac{\hbar^2}{2m} (\psi'(x_0 + 0) – \psi'(x_0 – 0)) -Z\psi(x_0) = 0 $$

$$\frac{\psi'(x_0 – 0)}{\psi(x_0)} – \frac{\psi'(x_0 + 0)}{\psi(x_0)} = -\frac{2mZ}{\hbar^2}$$

となる。故に\(k_0 = -\frac{mZ}{\hbar^2}\)

　ポテンシャルによる束縛状態を考えているので、\(E<0\)である。\(x \neq x_0 = 0\)の領域でシュレディンガー方程式を解くと、

$$\psi (x) = A_1e^{\kappa x} + A_2e^{-\kappa x} \hspace{4mm} \left( \kappa = \frac{\sqrt{-2mE}}{\hbar}\right)$$

が得られる。波動関数の有界性（\(x \rightarrow \pm \infty\)で\(\psi(x) \rightarrow 0\)）を考えると

$$\begin{align}\psi (x) &= Ae^{-\kappa |x|} = \left\{\begin{matrix} Ae^{\kappa x} & (x<0)\\ Ae^{-\kappa x} & (x>0)\end{matrix}\right. \end{align}$$

と書ける。接続条件式(iii)から

$$\frac{\psi'( – 0)}{\psi(0)} – \frac{\psi'(+ 0)}{\psi(0)} = 2k_0$$

$$\kappa A + \kappa A = 2k_0 A$$

$$\kappa = k_0 $$

となるので、

$$\kappa^2 = k_0^2 = \frac{-2mE}{\hbar} \rightarrow E = – \frac{\hbar^2 k_0^2}{2m}$$

が得られる。また、波動関数は

$$\begin{align}\psi_0 (x) &= Ae^{-k_0 |x|} = \left\{\begin{matrix} Ae^{k_0 x} & (x<0)\\ Ae^{-k_0 x} & (x>0)\end{matrix}\right. \end{align}$$

$$V(x) = -Z \delta (x – a)-Z \delta (x + a) \tag{iv}$$

　第一励起状態\(\psi_2\)のエネルギー固有値が正となる場合の\(a = a_0\)を探せば良い。\(\psi_2\)は奇関数なので、束縛状態の波動関数は

$$\begin{align}\psi_2 (x) = \left\{\begin{matrix} Ae^{\kappa x} & (x<-a)\\Be^{\kappa x}- Be^{-\kappa x}& (-a<x<a) \\-Ae^{-\kappa x} & (x>a)\end{matrix}\right. \end{align}$$

と書ける。\(x =-a\)での境界条件から

$$\begin{align}Ae^{-\kappa a} &= Be^{-\kappa a}- Be^{\kappa a} \end{align}$$

$$\begin{align} \kappa Ae^{-\kappa a} – \kappa (Be^{-\kappa a}+ Be^{\kappa a} ) &= 2k_0 Ae^{-\kappa a}\end{align}$$

が得られる。これを行列に変形すると

$$\begin{align} \begin{pmatrix} e^{-\kappa a} & e^{\kappa a} -e^{-\kappa a} \\ (2k_0 – \kappa)e^{-\kappa a} & \kappa (e^{\kappa a} +e^{-\kappa a} )\end{pmatrix} \begin{pmatrix} A\\B\end{pmatrix}= 0\end{align}$$

となる。非自明な解(\(A\neq 0 , B\neq 0\))を持つには

$$\begin{align} \begin{pmatrix} e^{-\kappa a} & e^{\kappa a} -e^{-\kappa a} \\ (2k_0 – \kappa)e^{-\kappa a} & \kappa (e^{\kappa a} +e^{-\kappa a} )\end{pmatrix} = 0\end{align}$$

となれば良い。これを変形すると

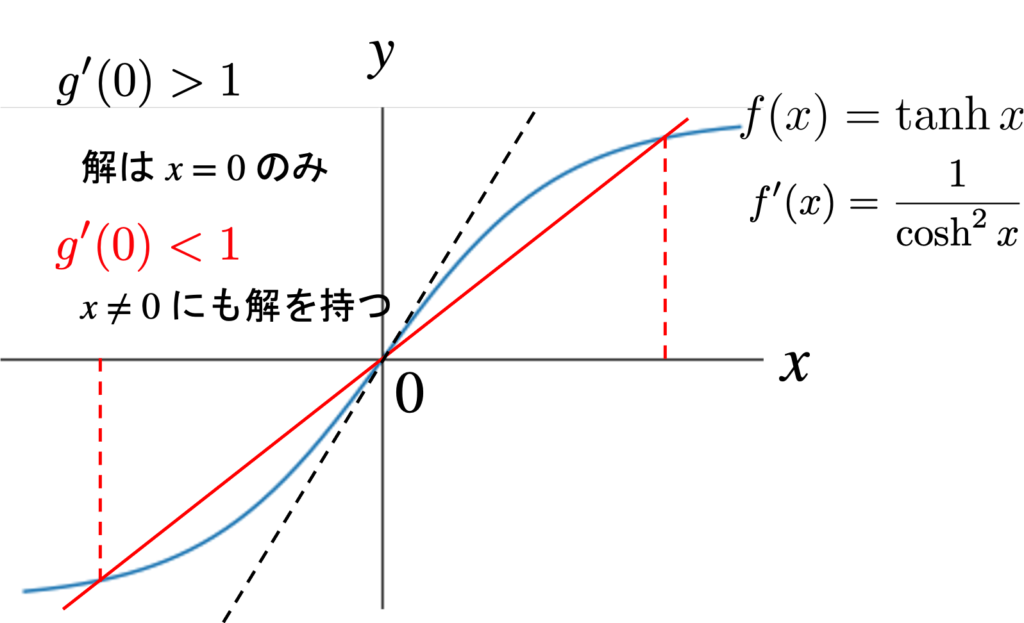
$$\tanh \kappa a = \frac{\kappa}{2k_0 – \kappa} = \frac{\kappa a}{2k_0 a- \kappa a} \tag{*}$$

となる。式(\(*\))について、\(f(\kappa a) = \tanh \kappa a\)と\(g(\kappa a) = \frac{\kappa a}{2k_0 a- \kappa a}\)の交点が解となる。\(f'(\kappa a = 0) = 1\)であるので、\(g'(\kappa a = 0) >1 \)なら自明な解のみになり、\(g'(\kappa a = 0) <1 \)ならば非自明な解も持つ。よって、

$$g'(\kappa a)= \frac{2k_0 a}{(2k_0 a- \kappa a)^2} $$

$$g'(0)= \frac{1}{2k_0 a} < 1 $$

$$a < \frac{1}{2k_0 } = a_0 $$

　前問と同様に計算する。\(\psi_1\)は偶関数なので、束縛状態の波動関数は

$$\begin{align}\psi_1 (x) = \left\{\begin{matrix} Ae^{\kappa x} & (x<-a)\\Be^{\kappa x} + Be^{-\kappa x}& (-a<x<a) \\Ae^{-\kappa x} & (x>a)\end{matrix}\right. \end{align}$$

と書ける。\(x =-a\)での境界条件から

$$\begin{align}Ae^{-\kappa a} &= Be^{-\kappa a}+ Be^{\kappa a} \end{align}$$

$$\begin{align} \kappa Ae^{-\kappa a} – \kappa (Be^{-\kappa a}- Be^{\kappa a} ) &= 2k_0 Ae^{-\kappa a}\end{align}$$

が得られる。これを行列に変形すると

$$\begin{align} \begin{pmatrix} e^{-\kappa a} & -(e^{\kappa a} +e^{-\kappa a}) \\ ( \kappa – 2k_0)e^{-\kappa a} & \kappa (e^{\kappa a} -e^{-\kappa a} )\end{pmatrix} \begin{pmatrix} A\\B\end{pmatrix}= 0\end{align}$$

となる。非自明な解(\(A\neq 0 , B\neq 0\))を持つには

$$\begin{align}\begin{pmatrix} e^{-\kappa a} & -(e^{\kappa a} +e^{-\kappa a}) \\ ( \kappa – 2k_0)e^{-\kappa a} & \kappa (e^{\kappa a} -e^{-\kappa a} )\end{pmatrix} = 0\end{align}$$

となれば良い。これを変形すると

$$\tanh \kappa a = \frac{2k_0 }{\kappa} -1 = \frac{2k_0 }{k_1}-1 \tag{5}$$

　

　二つの原子をゆっくり引き離すと、束縛状態のエネルギー（波数）も微小変化する。この変化を\(a \rightarrow a + \delta a\)にすると\(\kappa \rightarrow \kappa + \delta \kappa\)になると表す。このとき、式(5)は

$$\tanh (\kappa + \delta \kappa) (a + \delta a) = \frac{2k_0 }{\kappa + \delta \kappa} – 1\tag{6}$$

となる。式(6)の左辺は

$$\begin{align}\tanh (\kappa + \delta \kappa) (a + \delta a)&\simeq \tanh (\kappa a + \delta \kappa a +\kappa \delta a) \\ &\simeq \tanh \kappa a + \frac{1}{\cosh^2 \kappa a}(\delta \kappa a +\kappa \delta a) \\ &= \tanh \kappa a (1-\tanh^2 \kappa a) (\delta \kappa a +\kappa \delta a)\end{align}$$

となり、右辺は

$$\frac{2k_0 }{\kappa + \delta \kappa} – 1 \simeq \frac{2k_0}{\kappa} \left(1- \frac{\delta \kappa}{\kappa} \right) -1$$

となる。これらの近似と、式(5)を用いて

$$\tanh \kappa a (1-\tanh^2 \kappa a) (\delta \kappa a +\kappa \delta a) \simeq \frac{2k_0}{\kappa} \left(1- \frac{\delta \kappa}{\kappa} \right) -1$$

$$\left(\frac{4k_0a }{\kappa} + \frac{2k_0 }{\kappa^2} – \frac{4k_0^2 a }{\kappa^2}\right)\delta \kappa = \left(\frac{4k_0^2 }{\kappa} – 4k_0\right)\delta a$$

が得られ、\(k_0 a \gg 1\)の元で

$$\frac{\delta \kappa}{\delta a} \simeq \left(\frac{4k_0^2 }{\kappa} – 4k_0\right)\left(\frac{4k_0a }{\kappa} – \frac{4k_0^2 a }{\kappa^2}\right)^{-1} \simeq -\frac{\kappa}{a} \tag{7}$$

となる。

　また、\(\delta a,\delta \kappa\)を無限小とすると

$$\begin{align}\frac{\delta \kappa}{\delta a} &= \frac{d \kappa}{d a} = \frac{d \kappa}{d E} \frac{d E}{d a} =\frac{d }{d E}\left(\frac{\sqrt{-2mE}}{\hbar} \right) \frac{d E}{d a}\\ &= -\frac{\sqrt{2m}}{\hbar} \sqrt{\frac{1}{-E}}\frac{d E}{d a}\\ &=-\frac{{2m}}{\hbar^2}\frac{1}{\kappa}\frac{d E}{d a} \tag{8}\end{align}$$

が得られる。よって、式(7)と(8)より

$$\frac{d E}{d a} = \frac{{2m}\kappa^2}{\hbar^2 a}$$

となる。

　ここで、\(k_0 a \gg 1\)の元では\(\tanh \kappa a \rightarrow 1\)となる（\(\tanh\)の性質）ので、式(*)より

$$\tanh \kappa a = \frac{\kappa}{2k_0 – \kappa} \simeq 1 \rightarrow \kappa \simeq k_0$$

が得られるので、

$$\frac{d E}{d a} \simeq \frac{{2m} k_0^2}{\hbar^2 a}$$

と書ける。従って、２つの原子間に働く力\(F\)は

$$F = -\frac{d E}{d a} \simeq -\frac{{2m} k_0^2}{\hbar^2 a}$$

であるので、これは引力である。